How fast can grammar-structured generation be?

Hello, this is Brandon Willard from .txt. Since we started .txt a few months back, we've been hard at work researching all the ways that structured generation can be used to improve the results obtained from LLMs. An important part of making sure that structured generation is truly useful in practice is guaranteeing that its costs are low enough for widespread use. Alongside that concern is the general "flexibility" of the structure being imposed.

Usually, performance and flexibility are a very tricky trade-off. A while back we wrote a paper describing how minimal run-time latency can be achieved for regular language/regex-structured generation (see here), but, in practice, the flexibility of context-free languages is often needed. In the paper we also hinted at an extension of the regular language approach to context-free languages.

I devised one complete implementation of such an extension that I'll briefly demonstrate in the following. This extension to context-free grammar-structured generation carries theoretical performance and scaling guarantees similar to the regular language/regex case, and we'll see this in the form of a negligible sub-millisecond average impact on generation.

For a preview, here's a side-by-side using llama.cpp:

Let's say we want output that takes the following form:

The following is a SQL statement that returns values from the "id" column of the "users" table:
```sql
select id from users
```

We'll use a model that we know is already capable of producing this kind of output due to its training data:

import torch

from outlines import models, generate

model = models.transformers("Salesforce/codegen-350M-mono", device="cuda")

First, we'll ask it to complete this prompt using unstructured generation starting from a select statement:

prompt = r"""The following is a SQL statement that returns values from the "id" column of the "users" table:
```sql
select"""

text_generator = generate.text(model)

rng = torch.Generator(device="cuda")
rng.manual_seed(789001)

res = text_generator(prompt, max_tokens=100, rng=rng)

print(prompt + res)

The following is a SQL statement that returns values from the "id" column of the "users" table:
```sql
select id, first_name, last_name, age from users
```
OR as follows:
```sql
INSERT INTO users
VALUES (95518,'Brad', 'Patel',30)
```

Note: An INSERT statement which already has an autoincrement column will have this
as the column value but will instead be ``generative`` in the method definition.
This can be most any sequence_of_values_appearing

The results are not bad, but also not great. Unstructured generation adds a lot more to the output than we implicitly needed or wanted.

We can do better with context-free grammar (CFG) structured generation by clarifying exactly the kind of output we want, while also leaving enough room for the model to generate useful results. More specifically, let's say we only want to produce one fenced SQL code block that fulfills the implication of the text preceding it.

Here's a formal grammar that expresses those constraints:

from structured_generation.parsing import PartialLark

cfg_str = r"""
%import .org.partial_sql.start -> start_sql_code

start: PROMPT code_block
code_block : "\n```sql\n" start_sql_code "\n```\n"

PROMPT : /.+/

%import common.WS
%ignore WS
"""

lp = PartialLark(cfg_str, parser="lalr", start="start", deterministic=True)

What we did in that grammar was state that we wanted arbitrary prompt text immediately followed by a single fenced Markdown-style code block containing only valid SQL. We accomplished the latter by importing a larger SQL grammar based on this.

This example demonstrates how grammars can be composed and how doing so can cover the requirements of a desired prompt and output format as well as contextual syntax constraints on specific parts of the output.

In order to sample according to this grammar, we create a CFG Guide that follows the outlines API. While a version of CFG-structured generation with the same class name already exists in outlines , we'll be using our in-house implementation here. At some point, we plan to open source an implementation of this approach, and the interface will likely be the same.

from structured_generation.guides import CFGGuide

cfg_guide = CFGGuide.from_cfg_string(cfg_str, model.tokenizer)

Here's an example confirming that we get the expected output:

from outlines.samplers import multinomial


cfg_generator = CFGSequenceGenerator(
    cfg_guide, model, multinomial(), device=model.device
)

rng = torch.Generator(device="cuda")
rng.manual_seed(789001)

res = cfg_generator(prompt, max_tokens=100, rng=rng)

print(prompt + res)

The following is a SQL statement that returns values from the "id" column of the "users" table:
```sql
select id, first_name, last_name, age from users
```

The results follow the grammar, as expected:

assert lp.parse_from_state(lp.parse(prompt + res), is_end=True)

We need to emphasize that the multinomial sampling being performed here has not been altered to account for the grammar constraints. The sampling is performed after the entire support (i.e. non-zero "score" tokens) has been determined via our approach. This means that all of the results shown here apply to any type of sampling step.

We're going to perform some adhoc profiling by monkey patching the method used to determine which tokens are allowed next (i.e. the support) during structured generation. This is the step that introduces all the latency in structured generation. The method is Guide.get_next_instruction, and you can reference the outlines source code to see that very little is done in this step during unstructured generation.

import time
from types import MethodType


def make_timed(generator, override_class=False):
    times = []

    _get_next_instruction = type(generator.fsm).get_next_instruction

    def timed_next_instruction(self, *args, **kwargs):
        t1 = time.perf_counter()
        res = _get_next_instruction(self, *args, **kwargs)
        t2 = time.perf_counter()
        times.append(t2 - t1)
        return res

    if override_class:
        type(generator.fsm).get_next_instruction = timed_next_instruction
    else:
        generator.fsm.get_next_instruction = MethodType(timed_next_instruction, generator.fsm)

    return times


text_times = make_timed(text_generator)
cfg_times = make_timed(cfg_generator, override_class=True)

Here are the unstructured timings:

import numpy as np


rng = torch.Generator(device="cuda")
rng.manual_seed(789001)

text_times.clear()

while len(text_times) < 500:
    _ = text_generator(prompt, max_tokens=100, rng=rng)

import pandas as pd

df = pd.DataFrame(text_times, columns=["unstructured_times"])

print(df.describe())

       unstructured_times
count        5.000000e+02
mean         3.639091e-06
std          5.821888e-07
min          2.871966e-06
25%          3.246125e-06
50%          3.467547e-06
75%          3.839901e-06
max          7.604947e-06

Here are the structured timings:

rng = torch.Generator(device="cuda")
rng.manual_seed(789001)

cfg_times.clear()

while len(cfg_times) < 500:
    res = cfg_generator(prompt, max_tokens=100, rng=rng)
    assert lp.parse(prompt + res)

import pandas as pd

df = pd.DataFrame(cfg_times, columns=["structured_times"])

print(df.describe())

       structured_times
count        506.000000
mean           0.000442
std            0.000256
min            0.000079
25%            0.000177
50%            0.000514
75%            0.000603
max            0.001234

As we can see, our CFG-structured generation adds on average sub-millisecond latencies, and it barely breaks a millisecond at maximum.

In the following, we'll take the latency considerations of our approach a bit further by using a grammar for the C programming language and comparing the results with llama.cpp's grammar-structured generation.

This example uses the CodeGemma model, which has one of the largest vocabularies at 256k tokens.

from llama_cpp import Llama

llm = Llama.from_pretrained(
    repo_id="google/codegemma-2b-GGUF",
    filename="*2b-f16.gguf",
    n_gpu_layers=-1,
    penalize_nl=False,
    verbose=True,
    n_threads=1,
)

First, we produce a sample for an unstructured C code completion. This will serve as a baseline for comparison.

llama_prompt_1 = """
// Complete the following C program that determines whether or not an integer is a prime number
int main() {

  int n, i, flag = 0;
  printf("Enter a positive integer: ");
  scanf("%d", &n);

  // 0 and 1 are not prime numbers
  // change flag to 1 for non-prime number
  if (n == 0 || n == 1)
    flag = 1;

  for (i = 2; i <= n / 2;"""

llama_seed_1 = 2392

llama_kwargs = {
    "max_tokens": 400,
    "temperature": 1.0,
    "top_p": 1.0,
    "min_p": 0.0,
    "repeat_penalty": 1.0,
    "seed": llama_seed_1,
    "stop": ["<|file_separator|>"],
}

# Just in case
llm.set_seed(llama_seed_1)

unstruct_res = llm.create_completion(
    llama_prompt_1,
    **llama_kwargs
)

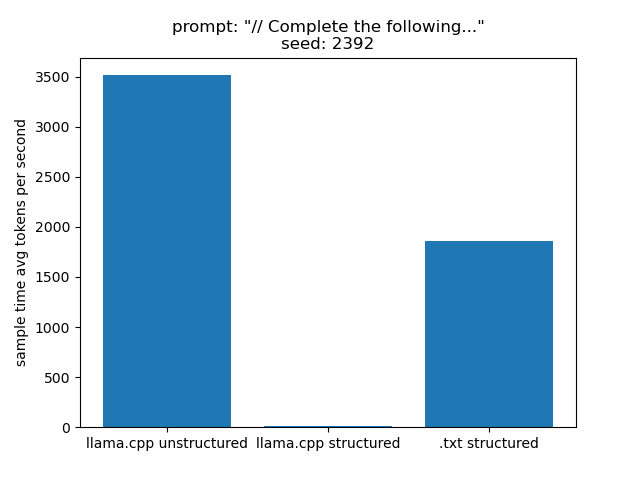
Llama.generate: prefix-match hit

llama_print_timings:        load time =      32.07 ms
llama_print_timings:      sample time =      33.30 ms /   117 runs   (    0.28 ms per token,  3513.20 tokens per second)
llama_print_timings: prompt eval time =       0.00 ms /     1 tokens (    0.00 ms per token,      inf tokens per second)
llama_print_timings:        eval time =     883.12 ms /   117 runs   (    7.55 ms per token,   132.48 tokens per second)
llama_print_timings:       total time =    3522.08 ms /   118 tokens

print(llama_prompt_1 + unstruct_res["choices"][0]["text"])

// Complete the following C program that determines whether or not an integer is a prime number
int main() {

  int n, i, flag = 0;
  printf("Enter a positive integer: ");
  scanf("%d", &n);

  // 0 and 1 are not prime numbers
  // change flag to 1 for non-prime number
  if (n == 0 || n == 1)
    flag = 1;

  for (i = 2; i <= n / 2; ++i) {

    // if n is divisible by i, then n is not prime
    // change flag to 1 for non-prime number
    if (n % i == 0) {
      flag = 1;
      break;
    }
  }

  // flag is 0 for prime numbers
  if (flag == 0)
    printf("%d is a prime number.", n);
  else
    printf("%d is not a prime number.", n);

  return 0;
}

Our approach is able to structure generation according to non-trivial context-free grammars and very large vocabularies with only a negligible cost. Likewise, these examples were performed using a large 256k vocabulary instead of the much smaller 32-50k vocabularies commonly used in grammar-structured generation benchmarks. We were also able to demonstrate a large practical advantage for our approach over llama.cpp's low-level C++ implementation within its own framework and amid multiple disadvantages (e.g. a much larger grammar, a sample sequence visiting more parse states).

Finally, it's time to explain another important detail about our implementation: it's unoptimized pure Python. We've been focusing on correctness and breadth of grammar support, so our implementation hasn't been designed for performance yet. We have numerous optimizations lined up that will bring down the latency significantly. We also have natural extensions to non-deterministic context-free grammars, non-trivial lexer-level logic, and efficient semantic constraints.

In summary, expect to see even more from .txt!