Making Structured Generation Faster Than Unstructured
Introduction
At .txt we are constantly working on making structured generation better. Previously, we demonstrated how our indexing-based approach adds negligible overhead during inference time and far outperforms other methods of structured generation. We also mentioned how our formulation in terms of finite-state machines gives rise to some interesting optimization possibilities based on the structure of the solution space (a phenomenon we call coalescence), potentially making structured generation even faster than unstructured generation. Next, we illustrate the simplest example of a class of LLM-level optimizations mentioned in our seminal paper (Willard and Louf, 2023) that can do the same.
Whether it's based on context-free grammars or regular expressions, structured generation makes some token sequences impossible to express. This means that a lot of computations in the layers of the LLM itself are unnecessary and can be skipped. Moreover, unlike coalescence, this is a "lossless" optimization that does not alter the results at all. In today's blog post, we will explain how this technique works, and we will present some benchmarks to support our case that structured generation can be faster than unstructured generation.
Motivation
Let's assume we are using a JSON schema to generate characters for a role-playing game with specific properties such as armor and strength:
simple_schema = """{ "$defs": { "Armor": { "enum": ["leather", "chainmail", "plate"], "title": "Armor", "type": "string" } }, "properties": { "name": {"maxLength": 10, "title": "Name", "type": "string"}, "age": {"title": "Age", "type": "integer"}, "armor": {"$ref": "#/$defs/Armor"}, "strength": {"title": "Strength", "type": "integer"}\ }, "required": ["name", "age", "armor", "strength"], "title": "Character", "type": "object" }"""
Small models like Microsoft's Phi-1.5 can be used to generate meaningful output, but it is often tricky to get the output to conform to our schema. Structured generation will help us create 100% valid JSON that conforms to a specific schema all the time.
import torch from transformers import ( AutoModelForCausalLM, AutoTokenizer, set_seed, ) random_seed = 20397 device = "cuda" if torch.cuda.is_available() else "cpu" checkpoint = "microsoft/phi-1_5" tokenizer = AutoTokenizer.from_pretrained(checkpoint) model = AutoModelForCausalLM.from_pretrained(checkpoint, trust_remote_code=True).to(device)
First, let's try the character JSON schema with unstructured generation. Since we can't force the model to conform to our schema, we "prompt and pray".
simple_prompt = ''' // JSON description of characters with different names and properties. // Armor can be "leather", "chainmail", or "plate" character1 = {"name": "Gustavo", "age": 30, "armor": "plate", "strength": 10} character2 = '''
inputs = tokenizer.encode(simple_prompt, return_tensors="pt").to(device) set_seed(random_seed) outputs = model.generate( inputs, eos_token_id=tokenizer.eos_token_id, pad_token_id=tokenizer.eos_token_id, max_length=100, temperature=0.1, renormalize_logits=True, do_sample=True, ) print(tokenizer.decode(outputs[0]))
// JSON description of characters with different names and properties.
// Armor can be "leather", "chainmail", or "plate"
character1 = {"name": "Gustavo", "age": 30, "armor": "plate", "strength": 10}
character2 =
{
"name": "Gustavo",
"age": 30,
"armor": "chainmail",
"strength": 10
}
The result is valid JSON, but we had to write a detailed prompt and give an example. There is no formal guarantee that the result follows the schema, unlike with structured generation.
Faster structured generation
The key to structured generation is that we only sample from the set of allowed
next tokens. We use our open-source library outlines to build an efficient
"index" lookup structure based on the finite-state machine formulation of a regular expression.
This structure adds almost zero overhead to unstructured generation, and it can
conveniently be used with Huggingface transformers and other libraries for
inference. To learn how to use outlines in your projects, head over to the
documentation or our latest blog post on
Coding For Structured Generation with
LLMs.
The crucial observation that allows for our optimization is that most of the time, the set of admissible next tokens will be a small fraction of the entire vocabulary. There is simply no point in computing their scores, since they'll be masked away. Recall that in the final step of the forward pass, an embedded vector representation needs to be converted into a distribution over the vocabulary. This involves a costly matrix multiplication. In formal terms (see Formal Algorithms for Transformers), the computation of the score/logits distribution involves the "unembedding matrix" \(\mathbf{W_u} \in \mathbb{R}^{N_V \times d_e}\), where \(N_V\) is the vocabulary size and \(d_e\) the embedding dimension, and can be expressed as \(\mathbf{W_u} \mathbf{X}[:, \ell]\), where \(\mathbf{X}\) is the encoded token sequence of length \(\ell\); hence \(\mathbf{X}[:, \ell] \in \mathbb{R}^{d_e}\) is the embedding of the last input token after the forward pass through all the transformer layers.
This can be visually expressed as follows:
\begin{equation} \label{orgc0dc5c8} \left[ \begin{array}{c} \mathbf{W_u}[1, :] \\ \mathbf{W_u}[2, :] \\ \mathbf{W_u}[3, :] \\ \mathbf{W_u}[4, :] \\ \vdots \\ \mathbf{W_u}[N_V, :] \\ \end{array} \right] \mathbf{X}[:, \ell] = \left[ \begin{array}{rcl} \mathbf{W_u}[1, :] & \cdot & \mathbf{X}[:, \ell] \\ \mathbf{W_u}[2, :] & \cdot & \mathbf{X}[:, \ell] \\ \mathbf{W_u}[3, :] & \cdot & \mathbf{X}[:, \ell] \\ \mathbf{W_u}[4, :] & \cdot & \mathbf{X}[:, \ell] \\ & \vdots & \\ \mathbf{W_u}[N_V, :] & \cdot & \mathbf{X}[:, \ell] \\ \end{array} \right] \end{equation}Every element of the output vector (corresponding to a token in the vocabulary) is the result of a dot product of \(\mathbf{X}[:, \ell]\) and a row in the unembedding matrix. We can achieve a modest reduction in runtime by only performing the necessary dot products for the allowed next tokens, which we'll call selective multiplication.
Suppose only tokens \(1\) and \(3\) were allowed continuations. Then the computation would be simplified as follows:
\begin{equation} \label{org63721ef} \left[ \begin{array}{c} \color{green}{\mathbf{W_u}[1, :]} \\ \color{lightgrey}{\mathbf{W_u}[2, :]} \\ \color{green}{\mathbf{W_u}[3, :]} \\ \color{lightgrey}{\mathbf{W_u}[4, :]} \\ \vdots \\ \color{lightgrey}{\mathbf{W_u}[N_V, :]} \\ \end{array} \right] \mathbf{X}[:, \ell] = \left[ \begin{array}{rcl} \color{green}{\mathbf{W_u}[1, :]} & \color{green}{\cdot} & \color{green}{\mathbf{X}[:, \ell]} \\ & \color{lightgrey}{-\infty} & \\ \color{green}{\mathbf{W_u}[3, :]} & \color{green}{\cdot} & \color{green}{\mathbf{X}[:, \ell]} \\ & \color{lightgrey}{-\infty} & \\ & \vdots & \\ & \color{lightgrey}{-\infty} & \\ \end{array} \right] \end{equation}Obviously, \eqref{org63721ef} is a beneficial approach whenever the number of allowed tokens is much smaller than \(N_V\). We use an empirical heuristic to determine whether this optimization is useful or detrimental–due to the overhead caused by selecting rows and gathering the results. If the set of admissible next tokens is too large, we default to the original computations and apply a mask over the entire vocabulary to filter out the disallowed tokens. In practice, we see either very few admissible tokens (e.g. when a keyword or a specific field name is expected), or too many (e.g. when a free-form string is being generated).
Let's see how well structured generation does. We use a Python/PyTorch subclass of
PhiForCausalLM, CustomPhiForCausalLM, that implements structured generation with our selective
multiplication optimization:
model = CustomPhiForCausalLM.from_pretrained( checkpoint, tokenizer=tokenizer, index=simple_schema_index, device=device, ).to(device) inputs_structured = tokenizer.encode("character1 = ", return_tensors="pt").to(device) set_seed(random_seed) outputs = model.generate( inputs_structured, eos_token_id=tokenizer.eos_token_id, pad_token_id=tokenizer.eos_token_id, max_length=100, temperature=0.1, renormalize_logits=True, do_sample=True, ) print(tokenizer.decode(outputs[0]))
character1 = {"name": "John", "age": 30, "armor": "chainmail", "strength": 20}<|endoftext|>
Notice how we don't need a detailed prompt at all, and yet the result conforms to the schema! Structured generation doesn't need examples in the prompt in order to generate valid structure every single time. We even found that 1-shot structured generation performs as well as 8-shot unstructured generation in the GSM8K benchmark.
Let's make sure the results are the same when using the selective multiplication optimization:
model = CustomPhiForCausalLM.from_pretrained( checkpoint, tokenizer=tokenizer, index=simple_schema_index, device=device, optimize=True, ).to(device) set_seed(random_seed) outputs = model.generate( inputs_structured, eos_token_id=tokenizer.eos_token_id, pad_token_id=tokenizer.eos_token_id, max_length=100, temperature=0.1, renormalize_logits=True, do_sample=True, ) print(tokenizer.decode(outputs[0]))
character1 = {"name": "John", "age": 30, "armor": "chainmail", "strength": 20}<|endoftext|>
The results with and without optimization are guaranteed to be the same.
Benchmarks
We ran benchmarks on the above JSON schema as well as the following more complex one:
complex_schema = """{ "$schema": "http://json-schema.org/draft-04/schema#", "title": "Schema for a recording", "type": "object", "definitions": { "artist": { "type": "object", "properties": { "id": {"type": "number"}, "name": {"type": "string"}, "functions": { "type": "array", "items": {"type": "string"} } }, "required": ["id", "name", "functions"] } }, "properties": { "id": {"type": "number"}, "work": { "type": "object", "properties": { "id": {"type": "number"}, "name": {"type": "string"}, "composer": {"$ref": "#/definitions/artist"} } }, "recording_artists": { "type": "array", "items": {"$ref": "#/definitions/artist"} } }, "required": ["id", "work", "recording_artists"] }"""
In order to compare apples to apples, we made sure that both unstructured and structured generation would operate on the same token sequences. Generally, this is not the case because they do not sample from the same token distributions. To alleviate this, we generated responses conforming to the schema using structured generation and used those as "ground truth" sequences in all evaluations. In other words, we computed the scores/logits for each token in the ground truth sequences (i.e. we used "forced decoding"), which guarantees that the computations are the same in all cases. We then measured generation speed for every generated token sequence. The plots show average time per token as a function of how often our optimization was used.
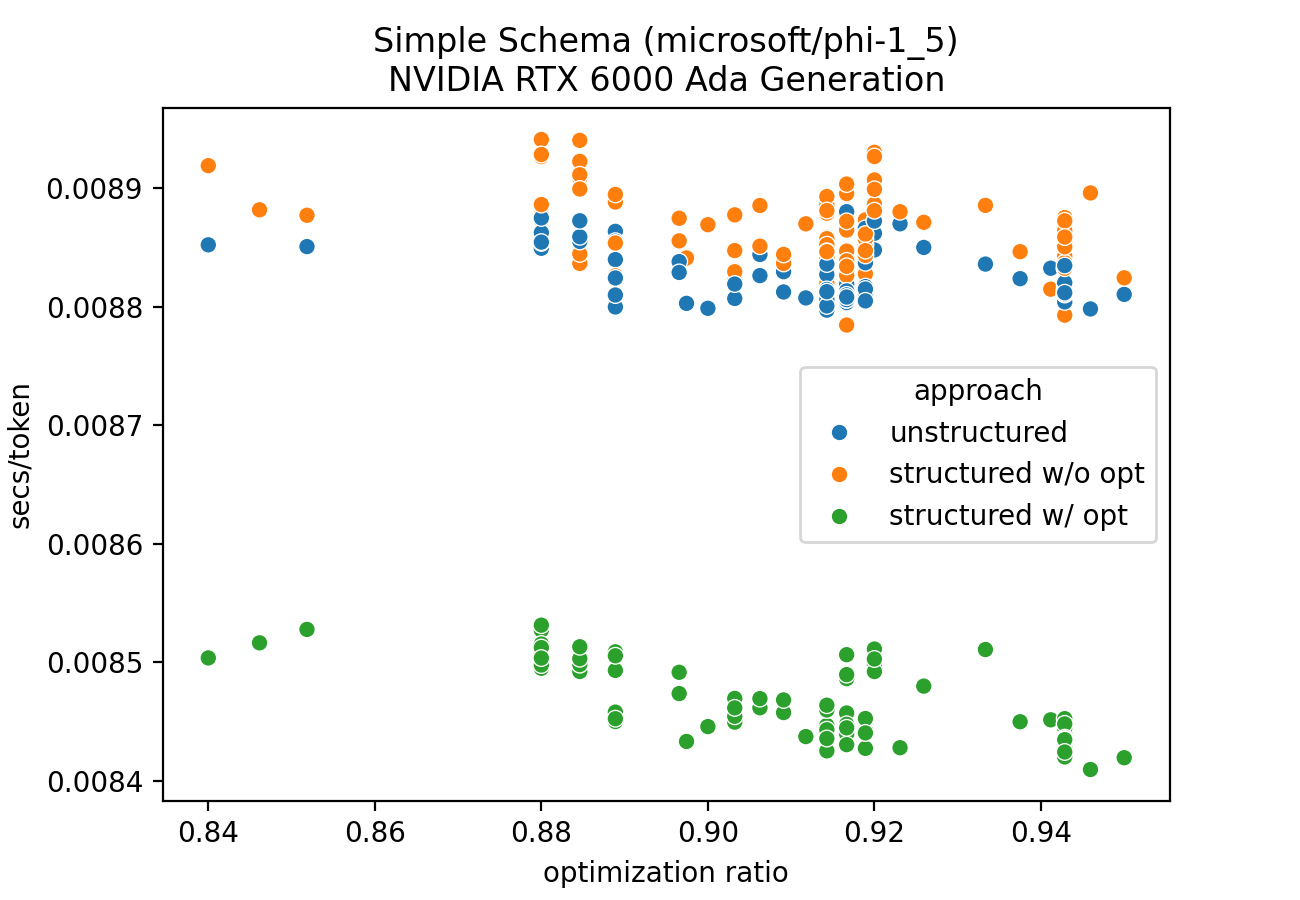
Figure 1: Simple schema GPU optimization ratio benchmark
Figure 1 shows that structured generation is always faster for the simple schema, since our selective multiplication optimization was used for the majority of tokens–as indicated by the "optimization ratio" (i.e. the percent of tokens in the sequence for which the optimization was applied).
On the token level, Figure 2 likewise shows that selective multiplication is beneficial compared to full multiplication whenever the number of allowed tokens is small; for larger token sets it incurs an overhead that we can easily avoid.
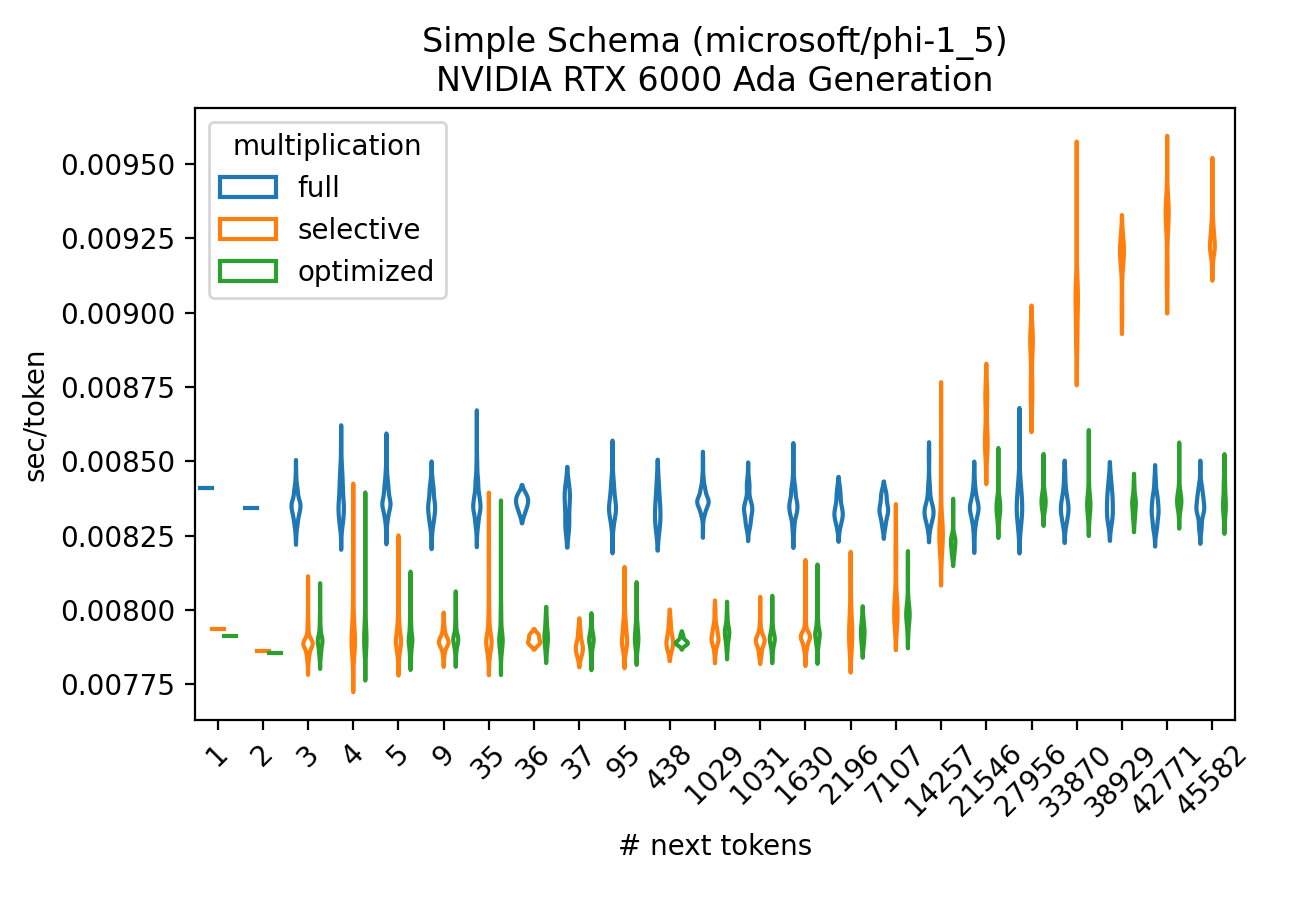
Figure 2: Simple schema GPU next tokens benchmark
For the complex schema, selective multiplication was used less often but still leads to significant savings. The results are given in Figures 3 and 4.
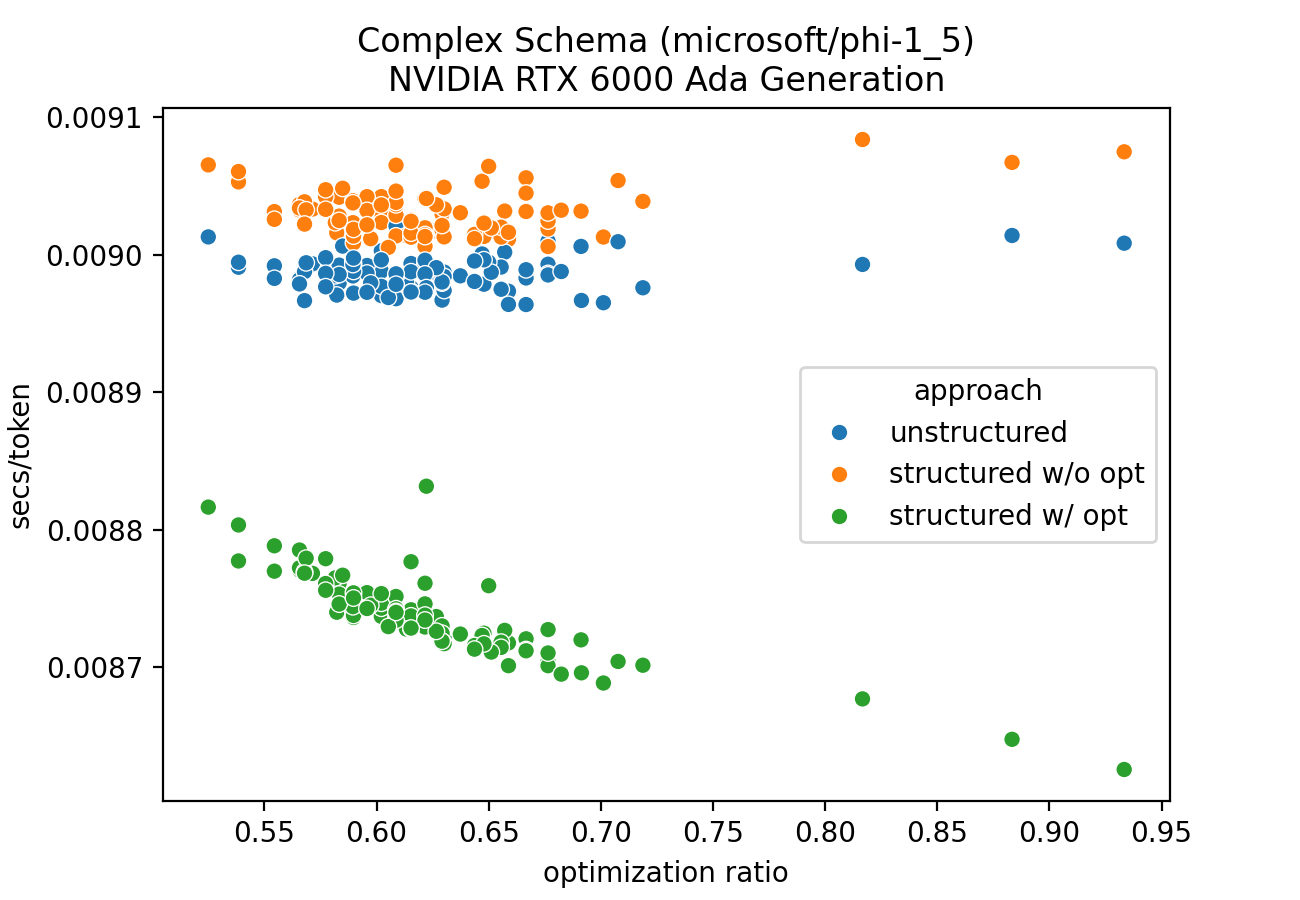
Figure 3: Complex schema GPU optimization ratio benchmark
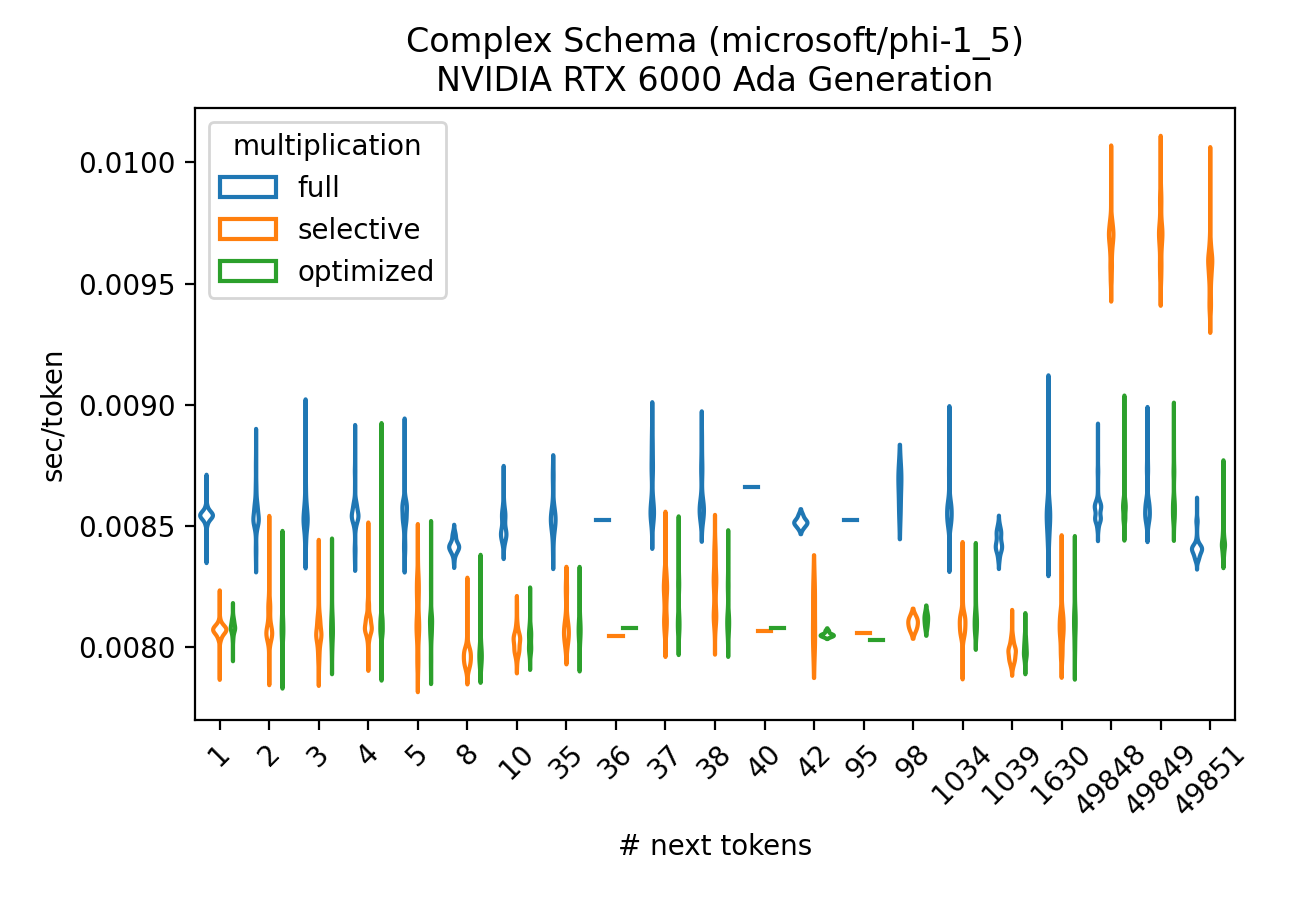
Figure 4: Complex schema GPU next tokens benchmark
Summary
With a single universally applicable model-level integration, we found that structured generation can be made faster than unstructured generation. While the differences are reasonably modest, they're consistent across the board. In other words, the results show that any overhead caused by structured generation can be more than recuperated by not having to compute logits for the entire vocabulary.
Also, just like our latency-focused context-free grammar post, this
implementation is in pure Python and uses no parallel/asynchronous computations,
so it includes a reasonable amount of unnecessary overhead that becomes even more
apparent at the sub-millisecond scales we observed. Instead of removing that
overhead in these examples, we opted keep it in and give a sense of the
average latency one might see in outlines, as well as show that
the optimization is still effective in such a setting.
This only scratches the surface of our work at .txt. We have more optimizations in this direction–and others–that go well beyond closing the performance gap between unstructured and structured generation. We can already see a future in which performing text generation with any amount of structure will be more advantageous than not.